Leetcode
Warning
The code in this page represents, essentially, a "code golf" solution to the problem statements. These solutions are not necessarily how I would code something in a production setting, as I tend to emphasize readability and maintainability over speed.
Array/String¶
Merged Sorted Array (easy)¶
Problem Statement¶
You are given two integer arrays nums1 and nums2, sorted in non-decreasing order, and two integers m and n, representing the number of elements in nums1 and nums2 respectively.
Merge nums1 and nums2 into a single array sorted in non-decreasing order.
The final sorted array should not be returned by the function, but instead be stored inside the array nums1. To accommodate this, nums1 has a length of m + n, where the first m elements denote the elements that should be merged, and the last n elements are set to 0 and should be ignored. nums2 has a length of n.
Example 1:
Input: nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
Output: [1,2,2,3,5,6]
Explanation: The arrays we are merging are [1,2,3] and [2,5,6].
The result of the merge is [1,2,2,3,5,6] with the underlined elements coming from nums1.
Example 2:
Input: nums1 = [1], m = 1, nums2 = [], n = 0
Output: [1]
Explanation: The arrays we are merging are [1] and [].
The result of the merge is [1].
Example 3:
Input: nums1 = [0], m = 0, nums2 = [1], n = 1
Output: [1]
Explanation: The arrays we are merging are [] and [1].
The result of the merge is [1].
Note that because m = 0, there are no elements in nums1. The 0 is only there to ensure the merge result can fit in nums1.
Constraints:
- nums1.length == m + n
- nums2.length == n
- 0 <= m, n <= 200
- 1 <= m + n <= 200
- -109 <= nums1[i], nums2[j] <= 109
Follow up: Can you come up with an algorithm that runs in O(m + n) time?
Solution¶
Intuition¶
Because we know that both arrays come pre-sorted, we can take advantage of the fact that i+1 will always be >= i for each array.
Approach¶
I decide to use a cursor-based approach. We will allocate a new slice of size m+n and use two individual cursors that point into each array respectively. Whenever we "consume" an element from either array, we'll increment the corresponding cursor. We'll need to account for edge cases where we have consumed all available values in a particular array.
Complexity¶
-
Time complexity: \(O(m+n)\)
-
Space complexity: \(O(m+n)\)
Code¶
func merge(nums1 []int, m int, nums2 []int, n int) {
merged := make([]int, m+n)
m_cursor := 0
n_cursor := 0
for i := 0; i < m+n; i++ {
if m_cursor >= m {
merged[i] = nums2[n_cursor]
n_cursor++
continue
}
if n_cursor >= n {
merged[i] = nums1[m_cursor]
m_cursor++
continue
}
// Asumption in this block is that both m_cursor < m and
// n_cursor < n. So we need to account for the cases where
// we've consumed all the values from one or the other
if nums1[m_cursor] < nums2[n_cursor] {
merged[i] = nums1[m_cursor]
m_cursor++
} else if nums2[n_cursor] < nums1[m_cursor] {
merged[i] = nums2[n_cursor]
n_cursor++
} else {
// they must be equal, so pick an element arbitrarily
merged[i] = nums1[m_cursor]
m_cursor++
}
}
for i := 0; i < m+n; i++ {
nums1[i] = merged[i]
}
}
Two Pointers¶
Valid Palindrome (easy)¶
Problem Statement¶
A phrase is a palindrome if, after converting all uppercase letters into lowercase letters and removing all non-alphanumeric characters, it reads the same forward and backward. Alphanumeric characters include letters and numbers.
Given a string s, return true if it is a palindrome, or false otherwise.
Example 1:
Input: s = "A man, a plan, a canal: Panama"
Output: true
Explanation: "amanaplanacanalpanama" is a palindrome.
Example 2:
Input: s = "race a car"
Output: false
Explanation: "raceacar" is not a palindrome.
Example 3:
Input: s = " "
Output: true
Explanation: s is an empty string "" after removing non-alphanumeric characters.
Since an empty string reads the same forward and backward, it is a palindrome.
Constraints:
- 1 <= s.length <= 2 * 105
- s consists only of printable ASCII characters.
Solution¶
Intuition¶
This is a fairly simple problem. We need to normalize the input string to disregard non-alphanumeric characters. There are a few ways you can do this, but I intend to use an approach that utilizes the least amount of data copying.
Approach¶
A naive approach would be to normalize the input string by copying each alphanumeric element into a new string and setting it to its lowercase representation. Then you could iterate over the normalized string and compare it to the opposing end of the string. However, this approach is costly as it requires lots of data copying and computation.
Instead, I used a cursor approach where we iterate over each element of the string. We will continue the loop if we found a non-alphanumeric character. Additionally, we keep track of the "opposing index" of the string, what we'll call oppositeCursor. In the for loop, the oppositeCursor is decremented until we find an alphanumeric character. Once that is found, we compare the lower-case representation at s[i] and s[oppositeCursor] and if they don't match, then it is not a valid palindrome.
Complexity¶
-
Time complexity: \(O(n)\)
-
Space complexity: \(O(1)\)
Code¶
func isPalindrome(s string) bool {
oppositeCursor := len(s)-1
for i := 0; i < len(s); i++ {
if i > oppositeCursor {
break
}
if !isAlphaNumeric(s[i]) {
continue
}
for;!isAlphaNumeric(s[oppositeCursor]) && i<oppositeCursor ; oppositeCursor-- {}
if i > oppositeCursor || strings.ToLower(string(s[i])) != strings.ToLower(string(s[oppositeCursor])) {
return false
}
oppositeCursor--
}
return true
}
func isAlphaNumeric(c byte) bool {
r := rune(c)
return unicode.IsLetter(r) || unicode.IsNumber(r)
}
Sliding Window¶
Minimum Size Subarray Sum (Medium)¶
Problem Statement¶
Given an array of positive integers nums and a positive integer target, return the minimal length of a subarray whose sum is greater than or equal to target. If there is no such subarray, return 0 instead.
Example 1:
Input: target = 7, nums = [2,3,1,2,4,3]
Output: 2
Explanation: The subarray [4,3] has the minimal length under the problem constraint.
Example 2:
Input: target = 4, nums = [1,4,4]
Output: 1
Example 3:
Input: target = 11, nums = [1,1,1,1,1,1,1,1]
Output: 0
Constraints:
1 <= target <= 109 1 <= nums.length <= 105 1 <= nums[i] <= 104
Follow up: If you have figured out the O(n) solution, try coding another solution of which the time complexity is O(n log(n)).
Solution¶
func minSubArrayLen(target int, nums []int) int {
minLength := 0
outerloop:
for left := 0; left < len(nums); left++ {
cumulativeSum += left
sum := 0
for right := left; right < len(nums); right++ {
sum += nums[right]
if sum >= target {
length := right - left + 1
if minLength == 0 || minLength > length {
minLength = length
}
continue outerloop
}
}
}
return minLength
}
Complexity Analysis
- Time: $O(n^2)
- The lefthand pointer of our subarray iterates over the entire
numsarray, which is \(O(n)\). - For every position of
left, we find every subarray starting from that point, which is \(O(n)\). - Together, these operations are multiplied to become \(O(n^2)\)
- Space: \(O(1)\)
| status | language | runtime | memory |
|---|---|---|---|
| Accepted | Go | 2884ms | 8.4MB |
func minSubArrayLen(target int, nums []int) int {
minLength := len(nums) + 1
sum := 0
left := 0
for right := 0; right < len(nums); right++ {
sum += nums[right]
for sum >= target {
minLength = min(minLength, right - left + 1)
sum -= nums[left]
left++
}
}
if minLength == len(nums) + 1 {
return 0
}
return minLength
}
| status | language | runtime | memory |
|---|---|---|---|
| Accepted | Go | 28ms | 7.8MB |
This solution uses a dynamically-sized array. We start with the smallest non-zero subarray at the lefthand side and increase the array until its total sum is greater than or equal to the target. Then, we increment the lefthand pointer until the sum is below the target again. During each iteration where we are incrementing the lefthand pointer, we set minLength equal to the current subarray length if it's smaller than the last recorded minLength.
The effect of this algorithm is that we only iterate over the entire subarray at most twice, which gives us \(O(n)\).
Matrix¶
Valid Sudoku (Medium)¶
Problem Statement¶
Determine if a 9 x 9 Sudoku board is valid. Only the filled cells need to be validated according to the following rules:
- Each row must contain the digits 1-9 without repetition.
- Each column must contain the digits 1-9 without repetition.
- Each of the nine 3 x 3 sub-boxes of the grid must contain the digits 1-9 without repetition.
Note:
A Sudoku board (partially filled) could be valid but is not necessarily solvable. Only the filled cells need to be validated according to the mentioned rules.
Solution¶
There are a few ways this could be solved. A naive solution would be to first iterate over every (x,y) coordinate in the puzzle, and for each coordinate, traverse the entire column at x and the entire row at y to see if an integer repeats. This algoirthm would require \(O(n^2)\) to iterate over every element, then \(O(2n)=O(n)\) to iterate over the respective column/row, for a total time complexity of \(O(n^3)\). The space complexity would be \(O(n)\) as we would want to allocate a set that contains the values seen in the entire column/row for (x,y).
Another solution would be as follows:
- Allocate two sets: one for every column, and one for every row. This gives a space complexity of \(O(n^2)\).
- Iterate over every
(x,y)coordinate. This gives time complexity of \(O(n^2)\) a. If a value is present in the coordinate, add the value to thecols[x]set, and to thecols[y]set. Time complexity is \(O(1)\) as hashing is constant time. b. If the value previously exists in either set, returnfalse. - If we made it through the entire puzzle and a value was not repeated for each
(col,row)tuple, then returntrue.
func isValidSudoku(board [][]byte) bool {
type set map[byte]struct{}
type index int
cols := make([]set, 9)
rows := make([]set, 9)
// The subBox that a particular coordinate belongs to is calculated using
// the formula: subBox = floor(x/3) + (floor(y/3) * 3). The constraint says
// that `board.length == 9` so we know there will always be 9 sub-boxes.
subBox := make([]set, 9)
boardLen := index(len(board))
for y := index(0); y < boardLen; y++ {
if rows[y] == nil {
rows[y] = set{}
}
for x := index(0); x < boardLen; x++ {
// Initialize the cols[x] set if it is nil
if cols[x] == nil {
cols[x] = set{}
}
// Calculate the 3x3 sub-box that we're in. If it doesn't exist,
// allocate it.
subBoxIdx := (x/index(3)) + ((y/index(3)) * 3)
subBoxElement := subBox[subBoxIdx]
if subBoxElement == nil {
subBoxElement = set{}
subBox[subBoxIdx] = subBoxElement
}
val := board[x][y]
if val == byte('.') {
continue
}
// Has this number been seen in this row before?
if _, existsInRow := rows[y][val]; existsInRow {
return false
}
rows[y][val] = struct{}{}
// Has this number been seen in this column before?
if _, existsCol := cols[x][val]; existsCol {
return false
}
cols[x][val] = struct{}{}
// Has this number been seen in our subBox before?
if _, existsInSubBox := subBox[subBoxIdx][val]; existsInSubBox {
return false
}
subBox[subBoxIdx][val] = struct{}{}
}
}
return true
}
| status | language | runtime | memory |
|---|---|---|---|
| Accepted | Go | 5ms (28.94%) | 3.4MB (35.58%) |
In this solution, our row/col/subBox hashmaps are stored inside an array of fixed length 9. We could have used a structure like map[index]set but because we know beforehand the values that would go into the map, it's more efficient to instead use an array of length 9: [9]set.
As you can see, this solution lies within the lower half percentile of all submissions in terms of runtime and memory performance. Perhaps there is a better way? I noticed one silly thing that was being done in my original solution: the initialization of the rows/copls/subBox sets were being done inside the main for loop. This means that there will be a lot of unnecessary branching done in the if statements that check if the set at a particular index had been initialized yet. Let's see how it performs with this change:
type set map[byte]struct{}
type index int
func isValidSudoku(board [][]byte) bool {
cols := make([]set, 9)
rows := make([]set, 9)
// The subBox that a particular coordinate belongs to is calculated using
// the formula: subBox = floor(x/3) + (floor(y/3) * 3). The constraint says
// that `board.length == 9` so we know there will always be 9 sub-boxes.
subBox := make([]set, 9)
boardLen := index(len(board))
for i := index(0); i < boardLen; i++ {
rows[i] = set{}
cols[i] = set{}
subBox[i] = set{}
}
for y := index(0); y < boardLen; y++ {
for x := index(0); x < boardLen; x++ {
// Calculate the 3x3 sub-box that we're in. If it doesn't exist,
// allocate it.
subBoxIdx := (x/index(3)) + ((y/index(3)) * 3)
val := board[x][y]
if val == byte('.') {
continue
}
// Has this number been seen in this row before?
if _, existsInRow := rows[y][val]; existsInRow {
return false
}
rows[y][val] = struct{}{}
// Has this number been seen in this column before?
if _, existsCol := cols[x][val]; existsCol {
return false
}
cols[x][val] = struct{}{}
// Has this number been seen in our subBox before?
if _, existsInSubBox := subBox[subBoxIdx][val]; existsInSubBox {
return false
}
subBox[subBoxIdx][val] = struct{}{}
}
}
return true
}
| status | language | runtime | memory |
|---|---|---|---|
| Accepted | Go | 0ms (100.00%) | 3.56MB (31.71%) |
As we can see, the runtime is now much better. However, being somewhat of a perfectionist, our memory consumption is still not where I'd like it to be. If you look at the Memory distribution for submissions, a large number of Leetcoders were able to get the usage down to ~2.6MB. Let's see what we can do to resolve this.
The two prior solutions are relying on a type set map[byte]struct{} to represent a set of bytes that we've seen. However, one property in this particular problem is that we already know the maximum size that this set could ever be, which is 9 (due to the fact that Sudoku cells can only be from 1-9). When we know the size of the hashmap beforehand, we can instead use a fixed-length array. We'll set the value of the array to be a bool, which in Go is a single byte.
type index int
func isValidSudoku(board [][]byte) bool {
cols := make([][9]bool, 9)
rows := make([][9]bool, 9)
// The subBox that a particular coordinate belongs to is calculated using
// the formula: subBox = floor(x/3) + (floor(y/3) * 3). The constraint says
// that `board.length == 9` so we know there will always be 9 sub-boxes.
subBox := make([][9]bool, 9)
boardLen := index(len(board))
for i := index(0); i < boardLen; i++ {
rows[i] = [9]bool{}
cols[i] = [9]bool{}
subBox[i] = [9]bool{}
}
for y := index(0); y < boardLen; y++ {
for x := index(0); x < boardLen; x++ {
// Calculate the 3x3 sub-box that we're in. If it doesn't exist,
// allocate it.
subBoxIdx := (x/index(3)) + ((y/index(3)) * 3)
val := board[x][y]
if val == byte('.') {
continue
}
valInt, _ := strconv.Atoi(string(val))
valInt--
// Has this number been seen in this row before?
if rows[y][valInt] {
return false
}
rows[y][valInt] = true
// Has this number been seen in this column before?
if cols[x][valInt] {
return false
}
cols[x][valInt] = true
// Has this number been seen in our subBox before?
if subBox[subBoxIdx][valInt] {
return false
}
subBox[subBoxIdx][valInt] = true
}
}
return true
}
| status | language | runtime | memory |
|---|---|---|---|
| Accepted | Go | 0ms (100.00%) | 2.66MB (73.09%) |
There's a way to make this even more memory efficient. For each row/col/box, we're storing a single bool for each integer 1-9. This totals to 9 bytes for each row/column/box. Ideally, we'd like to distill down our bool to a single bit, but there is no data type that is a single bit large. Instead, we could rely on bitmasking over a sufficiently sized data type (perhaps a uint16) to store our bool. Our data structures would look something like:
Notice that in this solution, I'll elect to use an array instead of a slice, as arrays take up even less memory in Go.
The bit mask is going to need to be equal to its location in the uint16, or more specifically, 1 << valInt
type index int
func isValidSudoku(board [][]byte) bool {
cols := [9]uint16{}
rows := [9]uint16{}
subBox := [9]uint16{}
valMap := map[byte]int{}
boardLen := index(len(board))
for y := index(0); y < boardLen; y++ {
for x := index(0); x < boardLen; x++ {
// Calculate the 3x3 sub-box that we're in. If it doesn't exist,
// allocate it.
subBoxIdx := (x/index(3)) + ((y/index(3)) * 3)
val := board[x][y]
if val == byte('.') {
continue
}
var valInt int
var exists bool
if valInt, exists = valMap[val]; !exists {
v, _ := strconv.Atoi(string(val))
v--
valMap[val] = v
}
valInt = valMap[val]
mask := (uint16(1)<<valInt)
// Has this number been seen in this row before?
if rows[y] & mask != 0 {
return false
}
rows[y] |= mask
// Has this number been seen in this column before?
if cols[x] & mask != 0 {
return false
}
cols[x] |= mask
// Has this number been seen in our subBox before?
if subBox[subBoxIdx] & mask != 0 {
return false
}
subBox[subBoxIdx] |= mask
}
}
return true
}
| status | language | runtime | memory |
|---|---|---|---|
| Accepted | Go | 0ms (100.00%) | 2.64MB (73.09%) |
While this solution is slightly more efficient with memory, it was barely noticable. For a 9x9 grid, we were able to shave off \((9+9+9)*(1*9) - (9+9+9)*1 = 216\) bytes (in the prior solution, each row/col/box required a single byte for each value 1-9, or 9 bytes total, but in this solution, each row/col/box needs only 2 bytes).
Hashmap¶
Group Anagram (Medium)¶
Problem Statement¶
Given an array of strings strs, group the anagrams together. You can return the answer in any order.
An Anagram is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once.
Example 1:
Input: strs = ["eat","tea","tan","ate","nat","bat"]
Output: [["bat"],["nat","tan"],["ate","eat","tea"]]
Example 2:
Input: strs = [""]
Output: [[""]]
Example 3:
Input: strs = ["a"]
Output: [["a"]]
Constraints:
- 1 <= strs.length <= 104
- 0 <= strs[i].length <= 100
- strs[i] consists of lowercase English letters.
Solution¶
In this problem, we are wanting to map words that contain the same letters into the same group. The intuition for this is that somehow the letters within the word are going to be used as a hash key into some sort of group. The first problem we run into is the fact that the hash is going to vary based on the order of the words, so we want our hashing function to be invariate to the letter ordering. An easy way to fix this is to simply sort the word alphabetically, then use that sequence of letters as the hash key.
You can see in the solution below that we do just that. We first allocate a groups dictionary that maps a string to a list. We iterate over every word in the strs variable, sort the word, then append that word to the list that it mapped to.
The problem requires us to return a list of a list of strings, so the last step is to modify the groups dictionary into the format the problem requires.
from typing import Dict
class Solution:
def groupAnagrams(self, strs: List[str]) -> List[List[str]]:
groups: Dict[str, list] = {}
for word in strs:
sorted_word = ''.join(sorted(word))
if sorted_word not in groups:
groups[sorted_word] = []
groups[sorted_word].append(word)
groups_list = []
for key, value in groups.items():
groups_list.append(value)
return groups_list
| status | language | runtime | memory |
|---|---|---|---|
| Accepted | Python | 90ms (88.31%) | 20.43MB (45.15%) |
We can simplify the logic of allocating the list in groups by using collections.defaultdict. Let's try that:
from typing import Dict
from collections import defaultdict
class Solution:
def groupAnagrams(self, strs: List[str]) -> List[List[str]]:
groups: Dict[str, list] = defaultdict(list)
for word in strs:
sorted_word = ''.join(sorted(word))
groups[sorted_word].append(word)
groups_list = []
for key, value in groups.items():
groups_list.append(value)
return groups_list
| status | language | runtime | memory |
|---|---|---|---|
| Accepted | Python | 77ms (99.63%) | 20.52MB (42.00%) |
The runtime here is a bit of a red herring because I can run the same code multiple times and get wildly different results. For example, when I run a second time I get 88ms. So, it's hard to judge just how good a solution really is without running it multiple times.
Intervals¶
Merge Intervals (Medium)¶
Problem Statement¶
Given an array of intervals where intervals[i] = [starti, endi], merge all overlapping intervals, and return an array of the non-overlapping intervals that cover all the intervals in the input.
Example 1:
Input: intervals = [[1,3],[2,6],[8,10],[15,18]]
Output: [[1,6],[8,10],[15,18]]
Explanation: Since intervals [1,3] and [2,6] overlap, merge them into [1,6].
Example 2:
Input: intervals = [[1,4],[4,5]]
Output: [[1,5]]
Explanation: Intervals [1,4] and [4,5] are considered overlapping.
Constraints:
- 1 <= intervals.length <= 104
- intervals[i].length == 2
- 0 <= starti <= endi <= 104
Solution¶
This solution has a wide range of possibilities. A naive solution might be to create a hashmap whereby each integer value is mapped to the current "largest" interval. You iterate through every integer in the range to see if you are overlapping with another range. If you are, extend the range if appropriate and continue to the next interval. However, this solution is a bit of a non-starter because the time complexity would be \(O(n*m)\) where \(n\) is the number of intervals, and \(m\) is the size of the largest interval. The space complexity is also \(O(n*m)\) because the hashmap needs to store a mapping for every integer in every range.
Another solution we could try is to first sort the intervals by starting integer. Once sorted, we iterate through the intervals and check each successive interval to see if it overlaps with a prior interval. This would be \(O(n)\) because you have to iterate through the intervals once (to sort), then again to compare to the previous interval.
Let's try the second solution:
class Solution:
def merge(self, intervals: List[List[int]]) -> List[List[int]]:
sorted_intervals = sorted(intervals, key=lambda entry: entry[0])
# We initialize `ranges` with the first element in sorted_intevals.
# we can assume that `sorted_intervals` contains at least one element
# because of the constraints listed in the problem statement.
ranges: List[List[int]] = [sorted_intervals[0]]
current_interval = 0
# We start from index 1 because we already added the first element
# to ranges.
for interval in sorted_intervals[1:]:
prev_range_start = ranges[current_interval][0]
prev_range_end = ranges[current_interval][1]
cur_range_start = interval[0]
cur_range_end = interval[1]
if cur_range_start <= prev_range_end:
# We know we have an overlapping range.
if cur_range_end - prev_range_start >= prev_range_end - prev_range_start:
# If we were to extend the interval, we get a larger range.
ranges[current_interval][1] = cur_range_end
continue
ranges.append(interval)
current_interval += 1
return ranges
This performs quite well:
| status | language | runtime | memory |
|---|---|---|---|
| Accepted | Python | 116ms (99.21%) | 21.50MB (10.16%) |
Stack¶
Simplify Path (Medium)¶
Problem Statement¶
Given a string path, which is an absolute path (starting with a slash '/') to a file or directory in a Unix-style file system, convert it to the simplified canonical path.
In a Unix-style file system, a period '.' refers to the current directory, a double period '..' refers to the directory up a level, and any multiple consecutive slashes (i.e. '//') are treated as a single slash '/'. For this problem, any other format of periods such as '...' are treated as file/directory names.
The canonical path should have the following format:
- The path starts with a single slash '/'.
- Any two directories are separated by a single slash '/'.
- The path does not end with a trailing '/'.
- The path only contains the directories on the path from the root directory to the target file or directory (i.e., no period '.' or double period '..')
Return the simplified canonical path.
Example 1:
Input: path = "/home/"
Output: "/home"
Explanation: Note that there is no trailing slash after the last directory name.
Example 2:
Input: path = "/../"
Output: "/"
Explanation: Going one level up from the root directory is a no-op, as the root level is the highest level you can go.
Example 3:
Input: path = "/home//foo/"
Output: "/home/foo"
Explanation: In the canonical path, multiple consecutive slashes are replaced by a single one.
Constraints:
- 1 <= path.length <= 3000
- path consists of English letters, digits, period '.', slash '/' or '_'.
- path is a valid absolute Unix path.
Solution¶
class Solution:
def simplifyPath(self, path: str) -> str:
elems = path.split("/")
out_path = list()
cur_elem = 0
for elem in elems:
if elem == "..":
if len(out_path) > 0:
out_path.pop()
continue
if elem in ("", "."):
continue
out_path.append(elem)
return "/" + "/".join(out_path)
| status | language | runtime | memory |
|---|---|---|---|
| Accepted | Python | 34ms (89.48%) | 17.55MB (5.52%) |
Strings¶
Strong Password Checker (hard)¶
Problem Statement¶
A password is considered strong if the below conditions are all met:
- It has at least 6 characters and at most 20 characters.
- It contains at least one lowercase letter, at least one uppercase letter, and at least one digit.
- It does not contain three repeating characters in a row (i.e., "Baaabb0" is weak, but "Baaba0" is strong).
Given a string password, return the minimum number of steps required to make password strong. if password is already strong, return 0.
In one step, you can:
- Insert one character to password,
- Delete one character from password, or
- Replace one character of password with another character.
Example 1:
Input: password = "a"
Output: 5
Example 2:
Input: password = "aA1"
Output: 3
Example 3:
Input: password = "1337C0d3"
Output: 0
Constraints:
- 1 <= password.length <= 50
- password consists of letters, digits, dot '.' or exclamation mark '!'.
Solution¶
This problem is pretty fucked, and I admittedly struggled to get it. The check to determine if the password is strong is easy, but figuring out the minimum number of steps to make it strong is very difficult. My solution passed 44/53 test cases, which is still a B- mind you
from typing import List
class Solution:
def strongPasswordChecker(self, password: str) -> int:
too_short = len(password) < 6
too_long = len(password) > 20
has_lowercase_letter = False
has_uppercase_letter = False
has_digit = False
has_excessive_repeating_character = False
num_excessive_repeating_sequences = 0
num_excessive_contiguous_characters = 0
# Contains the character we've seen contiguously, and the number of times
# it has been contiguous
contiguous_character: List[string, int] | None = None
for char in password:
if char.isalpha():
if char.islower():
has_lowercase_letter = True
else:
has_uppercase_letter = True
if char.isnumeric():
has_digit = True
if not contiguous_character:
contiguous_character = [char, 1]
else:
if char == contiguous_character[0]:
contiguous_character[1] += 1
if contiguous_character[1] >= 3:
has_excessive_repeating_character = True
num_excessive_repeating_sequences += 1
contiguous_character = None
else:
contiguous_character = [char, 1]
is_strong = (
not too_short
and not too_long
and has_lowercase_letter
and has_uppercase_letter
and has_digit
and not has_excessive_repeating_character
)
if is_strong:
return 0
steps = 0
if too_long:
num_deleted = 0
while (
num_excessive_repeating_sequences > 0
and num_deleted < len(password) - 20
):
steps += 1
num_excessive_repeating_sequences -= 1
num_deleted += 1
print("deleted character from repeating sequence")
steps += len(password) - 20 - num_deleted
print("deleted character")
if too_short:
num_added = 0
while num_added < 6 - len(password):
if num_excessive_repeating_sequences > 0:
if not has_lowercase_letter:
has_lowercase_letter = True
print("added character in repeating sequence: lowercase")
elif not has_uppercase_letter:
has_uppercase_letter = True
print("added character in repeating sequence: uppercase")
elif not has_digit:
has_digit = True
print("added character in repeating sequence: digit")
else:
print("added character in repeating sequence: arbitrary")
num_excessive_repeating_sequences -= 1
elif not has_lowercase_letter:
has_lowercase_letter = True
print("added lowercase")
elif not has_uppercase_letter:
has_uppercase_letter = True
print("added uppercase")
elif not has_digit:
has_digit = True
print("added digit")
else:
print("added arbitrary")
num_added += 1
steps += 1
# We need to replace one character for each repeating
# sequence.
# By doing a replacement, we could also add missing upper/lower/digits
# if possible.
while num_excessive_repeating_sequences > 0:
if not has_lowercase_letter:
has_lowercase_letter = True
print("replaced repeating sequence with lowercase")
elif not has_uppercase_letter:
has_uppercase_letter = True
print("replaced repeating sequence with uppercase")
elif not has_digit:
has_digit = True
print("replaced repeating sequence with digit")
else:
print("replaced repeating sequence with arbitrary")
num_excessive_repeating_sequences -= 1
steps += 1
if not has_lowercase_letter:
has_lowercase_letter = True
steps += 1
print("replaced character with lowercase")
if not has_uppercase_letter:
has_uppercase_letter = True
steps += 1
print("replaced character with upper")
if not has_digit:
has_digit = True
steps += 1
print("replaced character with digit")
return steps
Binary Tree General¶
Construct Binary Tree from Preorder and Inorder Traversal (Medium)¶
Problem Statement¶
Given two integer arrays preorder and inorder where preorder is the preorder traversal of a binary tree and inorder is the inorder traversal of the same tree, construct and return the binary tree.
Example 1
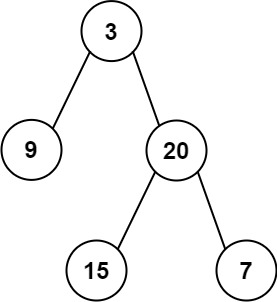
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]
Example 2
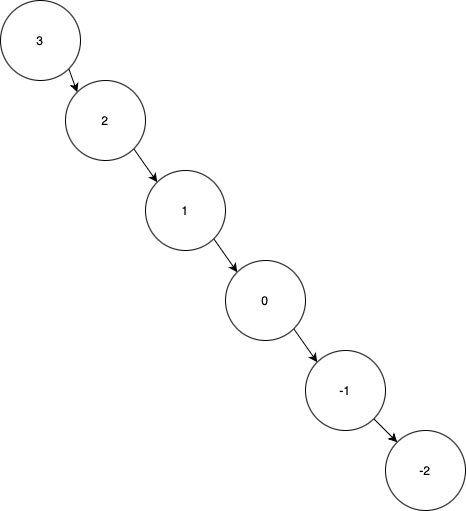
Input: preorder = [-1], inorder = [-1]
Output: [-1]
Solution¶
This question is asking us to create a data structure that represents the true shape of the tree, given the preorder and inorder traversals. For example, the Python3 code shows us this:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
What we need to determine is what nodes are children of what other nodes. To do this, we should look for some kind of pattern in how preorder/inorder traversals work. Let's remind ourselves of what preorder/inorder is:
Preorder: This first visits the current node, then it recurses into the left child, then into the right child.
Inorder: First it recurses into the left child, then it visits the current node, then recurses into the right child.
What we can guarantee is that a preorder traversal will always start with the root node. An in-order traversal will always give us the left-most node first. So we can do the simple part of first defining the root node:
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
root = TreeNode(val=preorder[0])
The next node in the preorder traversal is going to be the immediate left child (if it exists), then the right node (if it exists). How do we know if, in example 1, that 9 is a direct child of 3?
- 9 would have to be situated left of 3 in the in-order traversal, and
- 9 would have to be directly to the right of 3 in the pre-order traversal.
To test these two conditions, consider if we deleted node 9 and replaced 15 with the value 9. Then the traversals would look like this:
How do we know that 20 is a direct child of 3? It would have to satisfy the conditions:
20would need to occur right of3in the in-order traversal20needs to occur at a location that is exactly \(i+n\) away from3in the preorder traversal, where \(i\) is the index of3in the preorder list, and \(n\) is the number of elements in the left subtree. We can find \(n\) by subtracting the index of3in the in-order list from the index of9in the in-order list. We can hand-check this math in example 1: \(i=0\) and \(n=3-1=2\). We find that at index \(2\) in the pre-order list, we indeed find the value20.
Let's first create a naive implementation of this, just to check that our logic is sound. I fully expect that the runtime will be horrid, but that's okay for a proof of concept. Let's start with the simple case of populating the left subtree:
class Solution:
def buildTree(
self, preorder: List[int], inorder: List[int]
) -> Optional[TreeNode]:
if len(preorder) == 0:
return None
root = TreeNode(val=preorder[0])
if len(preorder) == 1:
return root
# Need to check if the next element in preorder is in the left subtree or the right
rootInorderIdx = inorder.index(preorder[0])
nextInorderIdx = inorder.index(preorder[1])
if nextInorderIdx < rootInorderIdx:
# We need to find the ending preorder index to pass to the bottom function. We can
# find this by including all the elements from preorder that appear to the left of 3
# in the inorder list.
maxPreorderIdx = 1
for elem in inorder[:rootInorderIdx]:
preorderIdx = preorder.index(elem)
if preorderIdx > maxPreorderIdx:
maxPreorderidx = preorderIdx
root.left = self.buildTree(
preorder=preorder[1:maxPreorderIdx],
inorder=inorder[:rootInorderIdx],
)
return root
What we're doing here is first creating the root node, which we know will always be the first element of preorder. Then, we know that the next element of preorder is going to be a direct left descendent if and only if that next element appears to the left in the inorder array. So, we do some simple checks to ensure this is true.
We run the code to see what happens and ensure that we receive the nodes [3, 9] in the output. Note, that this is obviously not the correct answer, but it will prove to us that the left subtree logic is working. The code above is confirmed to return [3, 9], so we can be reasonably confident the left subtree logic is working.
Now, let's move onto the right subtree logic.
- In order to get the right subtree from the inorder traversal, we need to find the index of the current root. The root is always
inorder[0](orroot.val, equivalently). So, we find the index that contains that value, and add one to it so we get the right subtree. - The next step is to find what node is the right child of the root. To do this, we need have to skip over all of the nodes from the left subtree. The information on what nodes are in the left subtree is contained in the inorder list: everything to the left of
3is the left subtree is the left, and everything to the right is the right subtree. We also know that the first element of the right subtree in the preorder traversal will be the root's direct descendent. So, loop over the values of preorder until we find the first right subtree element. - It's possible we didn't find any right children.
- We now know the index of the new subtree's root, and the right subtree. Pass these values into the recursive function call.
This solution passes the two test cases provided, so let's see if we get an accepted solution!
Wrong Answer
201 / 203 testcases passed
This is not a bad result because we got the vast majority of the cases. Let's inspect one of the failing test cases.
Input
preorder =
[3,2,1,0,-1,-2]
inorder =
[3,2,1,0,-1,-2]
Output
[3,null,2,null,1]
Expected
[3,null,2,null,1,null,0,null,-1,null,-2]
By constructing this tree by hand, we can tell that it's a tree with only right children. So why does the algorithm break after node 1?
It turns out, I made a really stupid mistake. In line 54 above, I'm checking the truthiness of rightChild instead of checking that it's not None. This means that the integer 0 would evaluate to False, which isn't what I intended. After fixing this, this test case now passed. However, we run into another problem: the last test case times out.
Our solution is doing some unoptimal things: we iterate over preorder and inorder multiple times linearly in various places. We can instead make use of sets to cut down on the \(O(n^2)\) operations we're doing (like for example in the cases where we're trying to determine the existence of a value in a particular subtree).
Another unoptimal thing we're doing is making judicious use of inorder.index to find the index of an element. We can instead create a hashmap (aka dict) to quickly find the location of the elements. We fix both of those issues here:
| status | language | runtime | memory |
|---|---|---|---|
| Accepted | Python | 663ms (5.03%) | 548.04 MB (5.25%) |
Our solution has now been accepted, but it's quite inefficient. Let's think critically about some of its shortcomings:
- We regenerate the
inorderIndexMapandpreorderIndexMapduring every step of recursion. Is there a way we can generate this once? - We iterate over the entire left subtree in this block to find the beginning of the right subtree. Do we have the information to not do that?
When fixing (1) above, we get a better memory result:
Note
class Solution:
def _buildTree(
self,
preorder: List[int],
inorder: List[int],
preorderOffset: int = 0,
inorderOffset: int = 0,
depth=0,
) -> Optional[TreeNode]:
if len(preorder) == 0:
return None
root = TreeNode(val=preorder[0])
if len(preorder) == 1:
return root
# Need to check if the next element in preorder is in the left subtree or the right
rootInorderIdx = self.inorderIndexMap[preorder[0]] - inorderOffset
nextInorderIdx = self.inorderIndexMap[preorder[1]] - inorderOffset
if nextInorderIdx < rootInorderIdx:
maxPreorderIdx = 1
for elem in inorder[:rootInorderIdx]:
preorderIdx = self.preOrderIndexMap[elem] - preorderOffset
if preorderIdx > maxPreorderIdx:
maxPreorderIdx = preorderIdx
root.left = self._buildTree(
preorder=preorder[1 : maxPreorderIdx + 1],
inorder=inorder[:rootInorderIdx],
preorderOffset=preorderOffset + 1,
inorderOffset=inorderOffset,
depth=depth + 1,
)
if len(inorder) < 2:
return root
rightSubtree = inorder[
self.inorderIndexMap[root.val] - inorderOffset + 1 :
]
rightSubtreeSet = set(rightSubtree)
rightChild = None
rightChildIdx = None
for idx, elem in enumerate(preorder[1:]):
if elem in rightSubtreeSet:
rightChild = elem
rightChildIdx = (
idx + 1
) # it's +1 because we've excluded the first element (which is the root)
break
if rightChild is not None:
root.right = self._buildTree(
preorder=preorder[rightChildIdx:],
inorder=rightSubtree,
preorderOffset=preorderOffset + rightChildIdx,
inorderOffset=inorderOffset
+ (len(inorder) - len(rightSubtree)),
depth=depth + 1,
)
return root
def buildTree(
self, preorder: List[int], inorder: List[int]
) -> Optional[TreeNode]:
self.inorderIndexMap = dict()
self.preOrderIndexMap = dict()
for idx in range(len(preorder)):
self.inorderIndexMap[inorder[idx]] = idx
self.preOrderIndexMap[preorder[idx]] = idx
return self._buildTree(preorder, inorder)
| status | language | runtime | memory |
|---|---|---|---|
| Accepted | Python | 436ms (5.03%) | 90.29 MB (36.34%) |
I'm going to leave the second optimization for another day, because this problem has already taken a huge number of hours of my day 
1D Dynamic Programming¶
Climbing Stairs¶
Problem¶
You are climbing a staircase. It takes n steps to reach the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
Example 1:
Input: n = 2
Output: 2
Explanation: There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps
Example 2:
Input: n = 3
Output: 3
Explanation: There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step
Constraints:
1 <= n <= 45
Thought Dump¶
This problem can be broken down into a series of subproblems. Each staircase can be thought of as being a linked chain of steps. Those steps can either be combined together so that we climb two steps at once, or they can remain by themselves. The goal here is to find the number of ways we could combine the steps together (or not combine them) to reach the nth step.
Let's take another example where n=4. The possible solutions are:
1. 1 + 1 + 1 + 1
2. 1 + 1 + 2
3. 2 + 2
4. 1 + 2 + 1
5. 2 + 1 + 1
What about when n=5?
1. 1 + 1 + 1 + 1 + 1
2. 1 + 1 + 1 + 2
3. 1 + 2 + 2
4. 2 + 1 + 2
5. 1 + 1 + 2 + 1
6. 2 + 2 + 1
7. 1 + 2 + 1 + 1
8. 2 + 1 + 1 + 1
Another way to look at this problem is in the links between the steps. Every flight of stairs will have n-1 links in them. We can model combining the links together through an array. Take for example n=5 above:
| 0 | 0 | 0 | 0 |
This array represents whether a pair of steps have been linked together, where 0 means "not linked" and 1 equals "linked". We can iterate through the possible ways these can be linked together. Note that in this model, we can't have two 1s directly adjacent to each other because that would mean we would have skipped over more than two steps at once. Going back to n=5, let's see the ways in which this can be done:
| 0 | 0 | 0 | 0 | # 1 + 1 + 1 + 1 + 1
| 0 | 0 | 0 | 1 | # 1 + 1 + 1 + (1+1)
| 0 | 1 | 0 | 1 | # 1 + (1+1) + (1+1)
| 1 | 0 | 0 | 1 | # (1+1) + 1 + (1+1)
| 0 | 0 | 1 | 0 | # 1 + 1 + (1+1) + 1
| 1 | 0 | 1 | 0 | # (1+1) + (1+1) + 1
| 0 | 1 | 0 | 0 | # 1 + (1+1) + 1 + 1
| 1 | 0 | 0 | 0 | # (1+1) + 1 + 1 + 1
To confirm the idea that the 1's can't be adjacent, let's try the n=4 example:
| 0 | 0 | 0 |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
This also checks out. The other pattern to note is that when we set a specific bit to 1, we've created a subproblem where we need to figure out how many combinations in the rest of the array we can have. Let's go back to the example of n=5, specifically this combination:
| 0 | 0 | 0 | 1 |
The subproblem is to figure out which of the remaining bits can be 1. We already know that the bit to the left of 1 can't be 1, so the subproblem is to figure out how many combinations can exist in n=3.
You can see how we can take advantage of dynamic programming to solve this. Let's consider the steps the program would take. Let's call n the number of steps, and l the number of links. l=n-1.
- Solve for
n=1, l=0: 1. - Solve for
n=2, l=1: 2. - Solve for
n=3, l=2:climbStairs(n=3) == climbStairs(n=2) + climbStairs(n=1)= 3. - Solve for
n=4, l=3:climbStairs(n=4) == climbStairs(n=3) + climbStairs(n=2)= 5. - Solve for
n=5, l=4:climbStairs(n=5) == climbStairs(n=4) + climbStairs(n=3)= 8.
Our calculations seem to work, so let's go ahead and implement it.
Solution¶
func climbStairs(n int) int {
prev1 := 1
prev2 := 1
answer := 1
for i := 2; i <= n; i++ {
answer = prev1 + prev2
prev2 = prev1
prev1 = answer
}
return answer
}
| status | language | runtime | memory |
|---|---|---|---|
| Accepted | Go | 1ms (78.30%) | 1.95 MB (49.19%) |
The distribution of runtime/memory is so tight that it doesn't seem there is much room for improvemet. This is probably going to be the best result we can get.
Backtracking¶
Letter Combinations of a Phone Number¶
Given a string containing digits from 2-9 inclusive, return all possible letter combinations that the number could represent. Return the answer in any order.
A mapping of digits to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.
Example 1:
Input: digits = "23"
Output: ["ad","ae","af","bd","be","bf","cd","ce","cf"]
Example 2:
Input: digits = ""
Output: []
Example 3:
Input: digits = "2"
Output: ["a","b","c"]
Thought dump¶
This problem involves finding all possible combinations of letters given a sequence of digits on a phone number pad. This can be thought of as a recursive problem, as we want to iterate over every possible letter for each digit, and prepend that letter to all the combinations found to the right of the current digit. The steps might look something like this:
- Grab the first digit in the string,
s[0] - Create a for loop that iterates over the possible letters for that digit
- For each iteration in the for loop, find the possible combinations of all remaining numbers in
s[1:] - Ensure base cases are accounted for, i.e. when
len(digits) == 0or when there are no remaining digits to the right.
We can take into consideration the fact that the length of the digits string is between 0 and 4 (inclusive), and that the digits can only be between 2 and 9 (inclusive).
Solution¶
var mapping map[byte][]string = map[byte][]string{
byte('2'): {"a", "b", "c"},
byte('3'): {"d", "e", "f"},
byte('4'): {"g", "h", "i"},
byte('5'): {"j", "k", "l"},
byte('6'): {"m", "n", "o"},
byte('7'): {"p", "q", "r", "s"},
byte('8'): {"t", "u", "v"},
byte('9'): {"w", "x", "y", "z"},
}
func letterCombinations(digits string) []string {
if len(digits) == 0 {
return []string{}
}
digit := digits[0]
if len(digits) == 1 {
return mapping[digit]
}
combinations := []string{}
subCombos := letterCombinations(digits[1:])
for _, char := range mapping[digit] {
for _, subCombo := range subCombos {
combinations = append(combinations, char + subCombo)
}
}
return combinations
}
| status | language | runtime | memory |
|---|---|---|---|
| Accepted | Go | 1ms (78.99%) | 2.08 MB (18.78%) |
Binary Tree BFS¶
Binary Tree Right Side View¶
Problem Statement¶
Given the root of a binary tree, imagine yourself standing on the right side of it, return the values of the nodes you can see ordered from top to bottom.
Example 1
Input: root = [1,2,3,null,5,null,4]
Output: [1,3,4]
Example 2:
Input: root = [1,null,3]
Output: [1,3]
Example 3:
Input: root = []
Output: []
Solution¶
Incorrect interpretation¶
I coded up a solution, but it turns out that my solution was incorrect because the problem statement is ambiguous. I interpreted the problem statement to mean that we want to always be looking to the right of the tree and return the nodes that appear farther right than the previous maximum "rightness" value we've seen. This means that we would want to keep track of the rightmost node as we're traversing the tree and add the nodes to the list that are greater than the previous maximum right. However, it appears this is not what the question is asking, and it appears I am not alone in my confusion. The Editorial states:
Quote
The problem is to return a list of the last elements from all levels, so it's way more natural to implement BFS here.
Nonetheless, here is my solution:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
# What does it mean to "see" the right nodes? Consider the tree:
# 1
# / \
# 2 3
# /
# 4
# \
# 5
# \
# 6
# Would we be able to see #6? I think the answer would be yes, as we are able to see
# only the nodes which appear to the _right_ of 3. In this case, we need to keep track of:
# 1. What's the farthest right node we've compile
# 2. What's the depth of the farthest right node we've seen?
# A node would be _visible_ if it is both farther right than the last previously seen node
# and it's at a lower depth. So as we traverse the tree, we want to keep track of the "rightness"
# and the depth of each node we've traversed.
#
# Proposed implementation:
# 1. Do a breadth first search
# 2. At every node, calculate the "rightness" and depth of the node. Initialize the "rightness" to 0
# and the depth to 0.
# 3. If the node we're iterating over has a "rightness" greater than the previous "rightness", then
# add that node to the list, and update the max "rightness" seen.
# Initialize our variables. The root node will always be visible.
if root is None:
return []
nodes = [root.val]
maxRight = 0
root.rightness = 0
nodesToIterate = [root]
while nodesToIterate:
curNode = nodesToIterate.pop(0)
if curNode.rightness > maxRight:
nodes.append(curNode.val)
if curNode.left:
left = curNode.left
left.rightness = curNode.rightness - 1
nodesToIterate.append(left)
if curNode.right:
right = curNode.right
right.rightness = curNode.rightness + 1
nodesToIterate.append(right)
return nodes
00:18:18
Correct solution¶
Given I had to peek at the editorial to figure out what the description meant, I attempted this a second time.
In this solution, we use BFS to iterate over each level individually. We keep track of the current level we're iterating at, and because we're iterating over the levels from left to right, we simply add each element to the end of the nodes list. When we've entered into a new level, we append a new element onto our list. Within a level, this will continue to overwrite the previous value such that only the rightmost value will not be overwritten. This is an efficient solution because we're taking advantage of how the BFS is ordered, because we know that the rightmost node will be iterated last at each level.
| status | language | runtime | memory | solution timer |
|---|---|---|---|---|
| Accepted | Python | 22ms (99.81%) | 16.56 MB (59.91%) | 00:15:01 |